| Aplicaciones de la Teledetección | |||
| Las aplicaciones de la Teledetección son múltiples y por tratarse de una tecnología reciente, todavía están en proceso de desarrollo. Las disciplinas que actualmente más utilizan las informaciones de los satélites son: geografía, biología, edafología, geología, agronomía, oceanografía, cartografía y arqueología.
Ejemplos de aplicaciones de la Teledetección
Algunas de las aplicaciones de la Teledetección más destacadas son:
Las figuras de esta página ilustran algunos de los usos menos conocidos de la Teledetección. Clicando sobre las imágenes accederás a la fuente de la información. |
Explotación de recursos naturales
Expansión urbana
Navegación y rescate marítimos
Arqueología y Teledetección
| ||
jueves, 30 de junio de 2016
SEMANA 16
SEMANA 15
Procesamiento digital de imágenes
El procesamiento digital de imágenes es el conjunto de técnicas que se aplican a las imágenes digitales con el objetivo de mejorar la calidad o facilitar la búsqueda de información.
Proceso de filtrado[editar]
Es el conjunto de técnicas englobadas dentro del preprocesamiento de imágenes cuyo objetivo fundamental es obtener, a partir de una imagen origen, otra final cuyo resultado sea más adecuado para una aplicación específica mejorando ciertas características de la misma que posibilite efectuar operaciones del procesado sobre ella.
Los principales objetivos que se persiguen con la aplicación de filtros son:
- Suavizar la imagen: reducir la cantidad de variaciones de intensidad entre píxeles vecinos.
- Eliminar ruido: eliminar aquellos píxeles cuyo nivel de intensidad es muy diferente al de sus vecinos y cuyo origen puede estar tanto en el proceso de adquisición de la imagen como en el de transmisión.
- Realzar bordes: destacar los bordes que se localizan en una imagen.
- Detectar bordes: detectar los píxeles donde se produce un cambio brusco en la función intensidad.
Por tanto, se consideran los filtros como operaciones que se aplican a los píxeles de una imagen digital para optimizarla, enfatizar cierta información o conseguir un efecto especial en ella.
El proceso de filtrado puede llevarse a cabo sobre los dominios de frecuencia y/o espacio.
Filtrado en el dominio de la frecuencia[editar]
Los filtros de frecuencia procesan una imagen trabajando sobre el dominio de la frecuencia en la Transformada de Fourierde la imagen. Para ello, ésta se modifica siguiendo el Teorema de la Convolución correspondiente:
- se aplica la Transformada de Fourier,
- se multiplica posteriormente por la función del filtro que ha sido escogido,
- para concluir re-transformándola al dominio espacial empleando la Transformada Inversa de Fourier.
Teorema de la Convolución (frecuencia): 

F(u,v): transformada de Fourier de la imagen original.
H(u,v): filtro atenuador de frecuencias.
Como la multiplicación en el espacio de Fourier es idéntica a la convolución en el dominio espacial, todos los filtros podrían, en teoría, ser implementados como un filtro espacial. Etapas del procesamiento de imágenes en el dominio de la frecuencia.
Etapas del procesamiento de imágenes en el dominio de la frecuencia.
 Etapas del procesamiento de imágenes en el dominio de la frecuencia.
Etapas del procesamiento de imágenes en el dominio de la frecuencia.Tipos[editar]
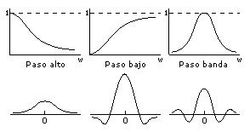
Existen básicamente tres tipos distintos de filtros que pueden aplicarse:
- Filtro paso bajo: atenúa las frecuencias altas y mantiene sin variaciones las bajas. El resultado en el dominio espacial es equivalente al de un filtro de suavizado, donde las altas frecuencias que son filtradas se corresponden con los cambios fuertes de intensidad. Consigue reducir el ruido suavizando las transiciones existentes.
- Filtro paso alto: atenúa las frecuencias bajas manteniendo invariables las frecuencias altas. Puesto que las altas frecuencias corresponden en las imágenes a cambios bruscos de densidad, este tipo de filtros es usado, porque entre otras ventajas, ofrece mejoras en la detección de bordes en el dominio espacial, ya que estos contienen gran cantidad de dichas frecuencias. Refuerza los contrastes que se encuentran en la imagen.
- Filtro paso banda: atenúa frecuencias muy altas o muy bajas manteniendo una banda de rango medio.
Ventajas[editar]
- Método simple y sencillo de implementar.
- Fácil asociación del concepto de frecuencia con ciertas características de la imagen; cambios de tonalidad suaves implican frecuencias bajas y cambios bruscos frecuencias altas.
- Proporciona flexibilidad en el diseño de soluciones de filtrado.
- Rapidez en el filtrado al utilizar el Teorema de la Convolución.
Desventajas[editar]
- Se necesitan conocimientos en varios campos para desarrollar una aplicación para el procesamiento de imágenes.
- El ruido no puede ser eliminado completamente.
Filtrado en el dominio del espacio[editar]
Las operaciones de filtrado se llevan a cabo directamente sobre los píxeles de la imagen. En este proceso se relaciona, para todos y cada uno de los puntos de la imagen, un conjunto de píxeles próximos al píxel objetivo con la finalidad de obtener una información útil, dependiente del tipo de filtro aplicado, que permita actuar sobre el píxel concreto en que se está llevando a cabo el proceso de filtrado para, de este modo, obtener mejoras sobre la imagen y/o datos que podrían ser utilizados en futuras acciones o procesos de trabajo sobre ella.
Los filtros en el dominio del espacio pueden clasificarse en:
- Filtros lineales (filtros basados en kernels o máscaras de convolución).
- Filtros no lineales.
El concepto de kernel se entiende como una matriz de coeficientes donde el entorno del punto (x,y) que se considera en la imagen para obtener g(x,y) está determinado por el tamaño y forma del kernel seleccionado. Aunque la forma y tamaño de esta matriz es variable y queda a elección de cada usuario, es común el uso de kernels cuadrados nxn. Dependiendo de la implementación, en los límites de la imagen se aplica un tratamiento especial (se asume un marco exterior de ceros o se repiten los valores del borde) o no se aplica ninguno. Es por ello, que el tipo de filtrado queda establecido por el contenido de dicho kernel utilizado. 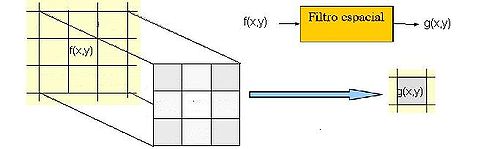

Para realizar un filtrado en el dominio del espacio se realiza una convolución (barrido) del kernel sobre la imagen. Para ello se sigue el Teorema de Convolución en el espacio: g(x,y) = h(x,y) * f(x,y)
- Cada píxel de la nueva imagen se obtiene mediante el sumatorio de la multiplicación del kernel por los píxeles contiguos:
g(x,y) = ∑∑ f(i,j) w(i,j) - Generalmente se divide sobre cierto valor constante para normalizar que suele obtenerse de la suma de los valores del kernel empleado.
Tipos[editar]
- Filtro paso bajo (suavizamiento): utilizados para eliminar ruido o detalles pequeños de poco interés puesto que sólo afecta a zonas con muchos cambios. La frecuencia de corte se determina por el tamaño del kernel y sus coeficientes. Se emplean diversos kernels:
- Promedio: promedio de píxeles vecinos (kernel de unos).
- Paso bajo en frecuencia.
- Media: reemplaza cada píxel por el valor medio de sus contiguos.
- Mediana: sustituye por el valor de la mediana de los píxeles vecinos (normalmente se comporta mejor que el de promedio).
- Gaussiano: aproximación a la distribución gaussiana.
- Filtro paso alto (atenuamiento): intensifica los detalles, bordes y cambios de alta frecuencia, mientras que atenúa las zonas de tonalidad uniforme. Esto permite una mejor identificación posterior de los objetos que se encuentren en la imagen, puesto que el brillo se hace mayor en las zonas con frecuencias más altas, al mismo tiempo que se oscurecen las zonas de frecuencias bajas. Es común la aparición de ruido tras el proceso.
- Realce de bordes por desplazamiento y diferencia: sustrae de la imagen original una copia desplazada de la misma. Así, es posible localizar y hacer resaltar los bordes existentes y que se quieran obtener según el modelo de kernel aplicado:
- Horizontal.
- Vertical.
- Horizontal/Vertical (diagonal).
- Realce de bordes mediante Laplace: este tipo de filtros realza los bordes en todas direcciones (los resultados que se obtienen pueden considerarse como una “suma” de los obtenidos tras aplicar todos los modelos del tipo anterior). En esta ocasión se trabaja con la segunda derivada, que permite obtener unos mejores resultados, a pesar del aumento del ruido que se produce en la imagen.
- Resalte de bordes con gradiente direccional: empleado para destacar y resaltar con mayor precisión los bordes que se localizan en una dirección determinada. Trabaja con los cambios de intensidad existentes entre píxeles contiguos.
- Detección de bordes y filtros de contorno (Prewitt y Sobel): al igual que los anteriores, se centra en las diferencias de intensidad que se dan pixel a pixel. Son utilizados para obtener los contornos de objetos y de este modo clasificar las formas existentes dentro de una imagen. Este tipo de filtros requieren un menor coste computacional.
Tratamiento de imagen por procesamiento de punto[editar]
Se trata de la mejora de la imagen considerando los métodos de procesamiento que se basan sólo en la intensidad de píxeles individuales. En lo que sigue llamaremos r y s a la intensidad de los píxeles antes y después del procesado. A continuacion se presentan ejemplos de tratamiento de imagen por procesamiento de punto utilizando el software de acceso libre ImageJ:
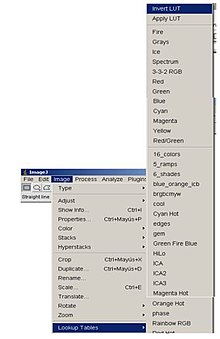
-Negativos de imágenes: La idea de esta transformación es invertir el orden de blanco a negro, de forma que la intensidad de la imagen de salida disminuya conforme la intensidad de la imagen de entrada aumente. Mediante ImageJ es sencillo realizar el negativo de una imagen. Ésta se conseguiría a partir de la Lookup Table, Invert LUT.
-Aumento del contraste:
La idea del aumento de contraste consiste en incrementar el rango dinámico de los niveles de gris de la imagen que se está procesando. La ubicación de los puntos (r1,s1) y (r2,s2) controla la forma de la función de transformación.
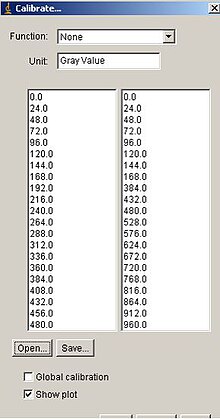
A partir de la opción "Calibrate" del ImageJ , diseño la función de transformación siguiente que me permite incrementar el contraste de la imagen original.
-Compresión del rango dinámico: Puede ocurrir que el rango dinámico de una imagen procesada excede la capacidad del dispositivo de presentación por lo que sólo veremos las partes más brillantes de la imagen. Una manera de comprimir el rango dinámico en realizar una transformación de este tipo:
s=C·log(1+| r | )
Utilizando de nuevo el ImageJ, podemos diseñar una función de la forma anterior que nos permita comprimir el rango dinámico de una imagen. En este caso se ha utilizado el Plugin "Expresion NT" , definiendo una función de la forma:
s=100.log(1+| r | )
-Fraccionamiento del nivel de gris: Si se desea destacar un rango específico del nivel de gris de una imagen. se puede por ejemplo adjudicar un valor alto a todos aquellos niveles de gris del rango de interés y uno bajo a los restantes.
-Fraccionamiento de los planos de bits: A veces puede desearse destacar la contribución que realizan a la imagen determinados bits específicos en vez de un rango determinado, es lo que se consigue con esta transformación.
SEMANA 14
ESTRUCTURA DE LOS DATOS:
| representación de datos raster El modelo raster es un método para el almacenamiento, el procesado y la visualización de datos geográficos . Cada superficie a representar se divide en filas y columnas, formando una malla o rejilla regular. Cada celda ha de ser rectangular, aunque no necesariamente cuadrada. Cada celda de la rejilla guarda tanto las coordenadas de la localización como el valor temático. La localización de cada celda es implícita, dependiendo directamente del orden que ocupa en la rejilla, a diferencia de la estructura vectorial en la que se almacena de forma explícita la topología. Las áreas que contienen idéntico atributo temático son reconocidas como tal, aunque las estructuras raster no identifican los límites de esas áreas como polígonos en sí.
Los datos raster son una abstración de la realidad, representan ésta como una rejilla de celdas o píxeles (ver figura 9), en la que la posición de cada elemento es implícita según el orden que ocupa en dicha rejilla. En el modelo raster el espacio no es continuo sino que se divide en unidades discretas. Esto le hace especialmente indicado para ciertas operaciones espaciales como por ejemplo las superposiciones de mapas o el cálculo de superficies.
Las estructuras raster pueden implicar en ocasiones un incremento del espacio de almacenamiento, ya que almacenan cada celda de la matriz sin tener en cuenta si se trata de una entidad o simplemente de un espacio “vacío”. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| tamaño y resolución de la celdilla/pixel
Pixel es la abreviatura de las palabras “picture element”. Es usada frecuentemente en teledetección para referirse a cada unidad de una imagen. En los SIG raster nos referimos a veces al pixel como la celda o el elemento base de una rejilla. El pixel/celda se refiere a la unidad mínima de información de una imagen o un mapa raster. Es el elemento más pequeño al que un dispositivo de visualización puede asignarle de forma independiente un atributo como es el color.
Tamaño del pixel y número de filas y columnas:
"El tamaño del pixel debe ser la mitad de la longitud más pequeña que sea necesario representar " Star and Estes (1990). A mayor tamaño de la celda, menor será el número de filas y columnas de la malla que cubre la superficie. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| estructuras de datos raster enumeración exhaustiva (figura 9) En esta estructura de datos el valor de cada pixel se registra individualmente, de forma que no se aplica ningún método de compresión cuando el mismo valor numérico aparece reiteradas veces seguidas.codificación por grupos de longitud variable "run-length" (figura 10) Es un método de compresión de imágenes. En el caso de que existan celdas contigüas con valores numéricos idénticos, esta estructura compacta la información. En vez de registrar el valor de cada celda individualmente, para cada fila se recoge el valor temático que existe y el número de celdas con dicho valor. Si sólo existe una celda con ese valor el tamaño se duplica, pero se reduce considerablemente en el caso de tres o más celdas idénticas. Cuanto mayores y más frecuentes sean las series de datos repetitivos, mayor compresión se logrará. Esta técnica es especialmente útil para codificar imágenes monocromo o binarias (Chrisman, 1997). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Figura 9. Enumeración exhaustiva | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Figura 10. Codificación "run-length" | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ventajas e inconvenientes de los modelos de datos raster y vectorial | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| entrada de datos | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Para más información consulta el módulo Entrada de Datos Geográficos | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
La entrada de datos en un SIG raster se puede realizar a partir de: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Imágenes de Satélite | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Digitalización manual
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Digitalización semi-automática | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Barredor óptico o escáner | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Rasterización de datos vectoriales | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| rasterización de datos vectoriales
Es el procedimiento a través del cual se convierten datos vectoriales (puntos, líneas y polígonos) a formato raster, formados éstos por celdas (píxeles) con un valor temático discreto en cada una. Es más sencillo que el procedimiento contrario, la conversión de datos raster a formato vectorial.
vectorización de datos rasterEs el procedimiento que convierte una imagen formada por celdas en un archivo vectorial. Puede o no incluir la creación de topología. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Para más información consulta el módulo Análisis Espacial Raster
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Pincha aquí para descargarte toda la teoría aparecida en este módulo
Píxel
«Pixels» redirige aquí. Para el cortometraje, véase Pixels (cortometraje).
Para la película, véase Pixels (película de 2015).
Un píxel o pixel,1 plural píxeles (acrónimo del inglés picture element, ‘elemento de imagen’), es la menor unidad homogénea en colorque forma parte de una imagen digital.
Índice[ocultar]Concepto[editar]
Ampliando lo suficiente una imagen (zoom) en la pantalla de una computadora, pueden observarse los píxeles que la componen. Los píxeles son los puntos de color (siendo la escala de grises una gama de color monocromática). Las imágenes se forman como una sucesión de píxeles. La sucesión marca la coherencia de la información presentada, siendo su conjunto una matriz coherente de información para el uso digital. El área donde se proyectan estas matrices suele ser rectangular. La representación del píxel en pantalla, al punto de ser accesible a la vista por unidad, forma un área homogénea en cuanto a la variación del color y densidad por pulgada, siendo esta variación nula, y definiendo cada punto sobre la base de la densidad, en lo referente al área.
En las imágenes de mapa de bits, o en los dispositivos gráficos, cada píxel se codifica mediante un conjunto de bits de longitud determinada (la profundidad de color); por ejemplo, puede codificarse un píxel con un byte (8 bits), de manera que cada píxel admite hasta 256 variaciones de color (28 posibilidades binarias), de 0 a 255. En las imágenes llamadas de color verdadero, normalmente se usan tres bytes (24 bits) para definir el color de un píxel; es decir, en total se pueden representar unos 224 colores, esto es 16.777.216 variaciones de color. Una imagen en la que se utilicen 32 bits para representar un píxel tiene la misma cantidad de colores que la de 24 bits, ya que los otros 8 bits son usados para efectos de transparencia.
Para poder visualizar, almacenar y procesar la información numérica representada en cada píxel, se debe conocer, además de la profundidad y brillo del color, el modelo de color que se utiliza. Por ejemplo, el modelo de color RGB (Red-Green-Blue) permite crear un color compuesto por los tres colores primarios según el sistema de mezcla aditiva. De esta forma, según la cantidad de cada uno de ellos que se use en cada píxel será el resultado del color final del mismo. Por ejemplo, el color magenta se logra mezclando el rojo y el azul, sin componente verde (este byte se pone en 0). Las distintas tonalidades del mismo color se logran variando la proporción en que intervienen ambas componentes (se altera el valor de esos dos bytes de color del píxel). En el modelo RGB lo más frecuente es usar 8 bits al representar la proporción de cada una de las tres componentes de color primarias. Así, cuando una de las componentes vale 0, significa que ella no interviene en la mezcla y cuando vale 255 (28 – 1) significa que interviene dando el máximo de ese tono, valores intermedios proveen la intensidad correspondiente.
La mayor parte de los dispositivos que se usan con una computadora (monitor, escáner, etc.) usan el modelo RGB (modelo de reflexión o aditivo), excepto los que aportantintes, como las impresoras, que suelen usar el modelo CMYK (modelo sustractivo).
Profundidad de color[editar]
Véase también: Profundidad de color
Un píxel, comúnmente, se representa con: 8 bits (28 colores), con 24 bits (224 colores, 8 bits por canal de color) o con 48 bits (248 colores); en fotografía avanzada y digitalización de imágenes profesional se utilizan profundidades aún mayores, expresadas siempre en valores de bits/canal de color en lugar de la suma de los tres canales. Los primeros son los más utilizados, reservando el de 8 bits para imágenes de alta calidad pero en tonos de grises, o bien con 256 colores en paleta seleccionada para baja calidad colorimétrica; el de 24 bits es el más común y de alta calidad, se lo utiliza en la mayoría de las imágenes fotográficas.
Múltiplos habituales[editar]Megapíxel[editar]
Véase también: Prefijos del SI
Un megapíxel o megapixel (Mpx) equivale a 1 millón de píxeles, a diferencia de otras medidas usadas en la computación en donde se suele utilizar la base de 1024 para los prefijos, en lugar de 1000, debido a su conveniencia respecto del uso del sistema binario. Usualmente se utiliza esta unidad para expresar la resolución de imagen de cámaras digitales; por ejemplo, una cámara que puede tomar fotografías con una resolución de 2048 × 1536 píxeles se dice que tiene 3,1 megapíxeles (2048 × 1536 = 3.145.728).
La cantidad de megapíxeles que tenga una cámara digital define el tamaño de las fotografías que puede tomar y el tamaño de las impresiones que se pueden realizar; sin embargo, hay que tener en cuenta que la matriz de puntos está siendo distribuida en un área bidimensional y, por tanto, la diferencia de la calidad de la imagen no crece proporcionalmente con la cantidad de megapíxeles que tenga una cámara, al igual que las x de una grabadora de discos compactos.
Las cámaras digitales usan componentes de electrónica fotosensible, como los CCD (del inglés Charge-Coupled Device) o sensores CMOS, que graban niveles de brillo en una base por-píxel. En la mayoría de las cámaras digitales, el CCD está cubierto con un mosaico de filtros de color, teniendo regiones color rojo, verde y azul (RGB) organizadas comúnmente según el filtro de Bayer, así que cada píxel-sensor puede grabar el brillo de un solo color primario. La cámara interpola la información de color de los píxeles vecinos, mediante un proceso llamado interpolación cromática, para crear la imagen final.
Para saber el número total de píxeles de una cámara, basta multiplicar el ancho de la imagen máxima que puede generar por el alto de la misma -desactivando previamente elzoom digital-; también es posible dividir el número de píxeles de ancho entre el número correspondiente al alto, y conocer la proporción de la imagen obtenida. Aquí se presenta una lista de las resoluciones comunes de cámaras digitales basándose en esta relación de aspecto:
Gigapíxel[editar]
Véase también: Prefijos del SI
Un gigapíxel (Gpx) equivale a un millardo o mil millones de píxeles, utilizando la base 1000 de los prefijos del sistema internacional, en vez de la base 1024 ISO/IEC 80000 oprefijo binario utilizados normalmente en el entorno de la informática. Usualmente se utiliza esta unidad para expresar la resolución de imagen de cámaras digitales.
Existen cámaras digitales capaces de realizar fotografías en gigapíxeles, como por ejemplo la ARGUS-IS de la Agencia de Proyectos de Investigación Avanzados de Defensa(DARPA)2 y la "super cámara" desarrollada por David Brady y su equipo de ingenieros de la Universidad de Duke
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Suscribirse a:
Entradas (Atom)